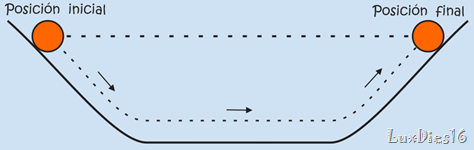
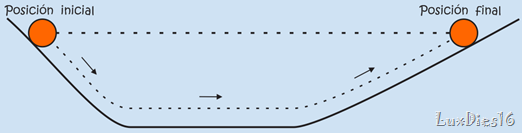
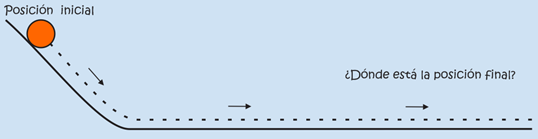
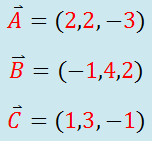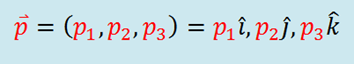Mundo Estudiante: Física

Mostrando entradas con la etiqueta Física. Mostrar todas las entradas

Primera Ley de Newton Del Movimiento

La idea aristotélica de que un objeto en movimiento debe estar impulsado por una fuerza continua fue demolida por Galileo, quien dijo que en ausencia de una fuerza, un objeto en movimiento continuará moviéndose. La tendencia de las cosas a resistir cambios en su movimiento fue lo que Galileo llamó inercia. Newton refinó esta idea de Galileo, y formuló su primera ley, que bien se llama ley e la inercia.

La palabra clave de esta ley es continúa haciendo lo que haga a menos que sobre él actué una fuerza. Si está en reposo continúa en un estado de reposo. Esto se demuestra muy bien cuando un mantel se retira con habilidad por debajo de una vajilla colocada sobre una mesa y los platos que dan en su estado inicial de reposo. La propiedad de los objetos de resistir cambios en su movimiento se llama Inercia.
Si un objeto se mueve, continúa moviéndose sin girar ni cambiar su rapidez. Esto se ve en las sondas espaciales que se mueven continuamente en el espacio exterior. Se deben imponer cambios del movimiento contra la tendencia de un objeto a retener su estado de movimiento. En ausencia de fuerzas netas, un objeto en movimiento tiende a moverse indefinidamente a lo largo de una línea recta.
¿Qué es la Fuerza Neta?
Una fuerza, en el sentido más sencillo, es un empuje o un tirón. Su causa puede ser gravitacional, eléctrica, magnética o simplemente esfuerzo muscular. Cuando sobre un objeto actúa más de una fuerza, lo que se considera es la fuerza neta, y ésta es la suma de todas las fuerzas.
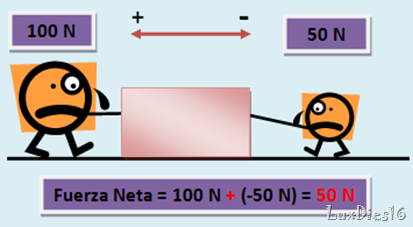
En la imagen siguiente se aplican fuerzas opuestas, para mover un cuerpo, al ser opuestas las fuerzas, una es positiva y otra negativa, pero estos signos solo sirven para indicar la dirección (direcciones opuestas, signos diferentes), y como ya se había dicho la fuerza neta es la suma de las fuerzas aplicadas. En este caso la fuerza neta es de 50 Newtons.

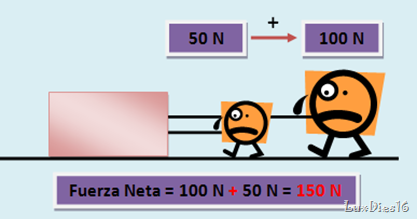
En la siguiente imagen se aplican fuerzas en la misma dirección, por lo tanto las dos tienen el signo positivo y sin ningún problema se suman las fuerzas para obtener la fuerza neta. En este caso a fuerza neta es de 150 N

En la siguiente imagen se aplican dos fuerzas de la misma magnitud en direcciones opuestas, y al ocurrir esto, la fuerza neta es cero, por lo tanto el objeto no se mueve.

>>Regla del Equilibrio<<

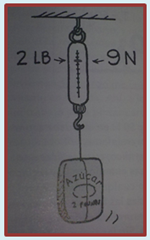
Si con un cordón atas una bolsa con 2 libras de azúcar y la cuelgas de una báscula de mano, el resorte de la báscula se estirará hasta que ésta indique 2 libras. El resorte estirado está bajo una “fuerza de estiramiento” llamada tención. Es probable que la misma báscula en un laboratorio científico indique que la misma fuerza es 9 newtons. Tanto las libras como los newtons son unidades de peso, que a su vez son unidades de fuerza. La bolsa de azúcar es atraída hacia la Tierra con una fuerza gravitacional de 2 libras, o lo que es igual, de 9 newtons. Si cuelgas dos bolsas de azúcar iguales a la primera, la lectura será de 18 newtons.
Nota que aquí son dos las fuerzas que actúan sobre la bolsa de azúcar: la fuerza de tensión que actúa hacia arriba, y su peso que actúa hacia abajo. Las fuerzas sobre la bolsa son iguales y en direcciones opuestas y se anulan; la fuerza neta es cero. Por consiguiente la bolsa permanece en reposo.
Cuando la fuerza neta que actúa sobre algo es cero, se dice que ese algo está en equilibrio mecánico. En notación matemática, la regla del equilibrio es:

Esto es, la suma vectorial de las fuerzas es igual a cero.

>>FUERZA DE SOPORTE<<

Imagina un libro que yace sobre una mesa. Ésta en equilibrio. ¿Qué fuerzas actúan sobre él? Una es la que se debe a la gravedad y que es su peso de libro. Como el libro esta en equilibrio, debe haber otra fuerza que actúa sobre él que haga que la fuerza neta sea cero: una fuerza hacia arriba opuesta a la fuerza de gravedad. La mesa es la que ejerce esa fuerza hacia arriba. A esta fuerza se le llama fuerza de soporte. Esta fuerza de soporte, hacia arriba, a menudo se llama fuerza normal y debe ser igual al peso del libro.

Es esta fuerza de soporte la que muestra tu peso. Cuando te pesas en una báscula de baño en reposo, la fuerza de soporte y la fuerza de gravedad que te jala hacia abajo tiene la misma magnitud. Por lo tanto decimos que tu peso es la fuerza de gravedad que actúa sobre ti.

Ejercicios:
--> ¿Cuál es la fuerza neta sobre un carro que es tirado con 100 libras hacia la derecha y con 30 libras hacia la izquierda?
-->¿La fuerza se puede expresar en libras y también en newtons?
-->¿Qué significa decir que algo está en equilibrio?
--> Un libro que pesa 15N descansa sobre una mesa plana. ¿Cuántos newtons de fuerza de soporte debe ejercer la mesa? ¿Cuál es la fuerza neta sobre el libro en este caso?
--> Cuando te paras sin moverte sobre una báscula de baño, ¿Cómo se compara tu peso con la fuerza de soporte de esta báscula?
Referencias:
Libro: Física Conceptual
Autor: Paul G. Hewitt
Editorial: Pearson Educación
Décima Edición

El Movimiento A Través De La Historia

Hace más de 2000 años, los antiguos científicos griegos estaban familiarizados con algunas de las ideas de la física que estudiamos en la actualidad.

-->El movimiento según Aristóteles (384-322 a. c.)

Aristóteles dividió el movimiento en dos clases principales: El movimiento natural y el movimiento violento.

Las afirmaciones de Aristóteles acerca del movimiento fueron el comienzo del pensamiento científico, y aunque él no creía que fueran definitivas acerca del tema, durante casi 2000 años sus seguidores consideraron sus ideas como fuera de toda duda. Aristóteles también decía que la Tierra no se movía, pues la Tierra debe estar en su lugar propio y como es inconcebible que haya una fuerza capaz de moverla, resultaba bastante claro que la Tierra no se movía.

-->Copérnico y la Tierra en movimiento.

En este ambiente intelectual Nicolás Copérnico (1473-1543), astrónomo polaco, formuló su teoría sobre el movimiento de la Tierra. Dedujo que la forma más sencilla de explicar los movimientos observados del Sol, la Luna y los planetas por el cielo es suponiendo que la Tierra y otros planetas describen círculos al rededor del Sol. Durante años desarrollo sus ideas sin hacerlas públicas, por dos razones fundamentales. La primera fue que tenía miedo de ser perseguido; una teoría tan distinta de la opinión común con seguridad se tomaría como un ataque al orden establecido. La segunda razón fue que él mismo tenía serias dudas, porque no podía reconciliar la idea de una Tierra en movimiento con las ideas que prevalecían acerca del movimiento. Finalmente, el los últimos días de su vida. Mandó a la imprenta su De Revolutionibus. El primer ejemplar de su famosa exposición llegó a él el día de su muerte: el 24 de mayo de 1543.

-->Galileo y la Torre inclinada.

Fue Galileo (1564-1642), el principal científico de principios del siglo XVII, quien dio crédito a la idea de Copérnico de una Tierra en movimiento. Lo logró desacreditando las ideas aristotélicas sobre el movimiento. Galileo demolió con facilidad la hipótesis de Aristóteles acerca de la caída de los cuerpos. Se dice que Galileo dejó caer objetos de varios pesos desde lo más alto de la Torre inclinada de Pisa, y luego comparó las caídas. Al contrario de la aseveración de Aristóteles, Galileo encontró que una piedra con el doble de peso que otra no caía con el doble de rapidez. A excepción del pequeño efecto de la resistencia del aire, encontró que los objetos de distinto peso, cuando se sueltan al mismo tiempo, caían untos y llegaban al suelo en el mismo momento.

--> Los planos inclinados de Galileo

Era básico para Aristóteles que un objeto requiere de un empuje o un tirón para mantenerse en movimiento. Y fue este principio básico el que rechazó Galileo al decir que si no hay interferencia para un objeto en movimiento, se mantendrá moviéndose en línea recta por siempre; no hace falta un empujón, ni tracción ni fuerza. Galileo demostró esta hipótesis experimentando con el movimiento de varios objetos sobre planos inclinados. Dedujo entonces que las esferas que ruedan por un plano horizontal ni se aceleran ni se desaceleran. La esfera llega al reposo finalmente no por su “Naturaleza”, sino por a fricción. Cuando avía menos fricción, el movimiento de los objetos duraba más. Dedujo que en ausencia de la fricción o de otras fuerzas contrarias, un objeto en movimiento horizontal continuaría moviéndose indefinidamente.

Galileo observó que una esfera, soltada desde el reposo en la parte superior de un plano inclinado hacia abajo, rodaba hacia abajo y después hacia arriba por la pendiente inclinada hacia arriba, hasta que casi llegaba a su altura inicial. Dedujo que sólo la fricción evitaba que subiera hasta llegar exactamente a la misma altura, porque cuanto más lisos fueran los planos, la esfera llegaría más cerca a la misma altura original.

A continuación redujo el ángulo del plano inclinado hacia arriba. De nuevo la bola subió casi hasta la misma altura, pero tuvo que ir más lejos. Con reducciones adicionales del ángulo obtuvo resultados parecidos: Para alcanzar la misma altura, la esfera tenía que llegar más lejos cada vez.

Entonces se preguntó: “si tengo un plano horizontal largo: ¿hasta donde debe llegar la esfera para alcanzar la misma altura inicial?”

Como el movimiento de bajada de la esfera en el primer plano es igual en todos los casos, su rapidez al comenzar a subir por el segundo plano es igual en todos los casos. Si sube por una pendiente más inclinada pierde su rapidez rápidamente. En una pendiente menos inclinada la pierde con más lentitud, y rueda durante mayor tiempo. Cuanto menor sea la pendiente de subida, con más lentitud pierde su rapidez.

En el tercer caso, cuando el plano es horizontal, la esfera no debería perder rapidez alguna. En ausencia de fuerzas de retardo, la tendencia de la esfera es a moverse por siempre sin desacelerarse. A la propiedad de un objeto de resistirse a los cambios en el movimiento la llamó INERCIA.

En 1642, varios meses después de la muerte de Galileo, nació Isaac Newton. A los 23 años ya había desarrollado sus famosas leyes de movimiento, que terminaron de demoler las ideas aristotélicas que habían dominado el razonamiento de los mejores pensadores durante casi dos milenios. Estas tres leyes las puedes encontrar más detalladas en las entradas que siguen de ésta, así como también en la entrada “La Dinámica y Leyes De Newton” de física I.

Te dejo un pequeño crucigrama para que retroalimentes la información anterior.

Referencias:

Libro: Física Conceptual

Autor: Paul G. Hewitt

Editorial: Pearson Educación

Décima Edición

Producto Punto, Escalar o Interno.

Recordemos que la palabra producto en términos matemáticos se refiere al resultado de multiplicar dos factores, pero en el caso de los vectores obtener su producto no es igual que al multiplicar dos números cualesquiera.

Se subdivide en varios productos:

a) Producto Escalar o interno (punto). Dados dos vectores A y B, su producto escalar o interno, A.B, se define como el producto de sus módulos por el coseno del ángulo que forman.

Por lo tanto:

Recuerda que el producto punto siempre será un escalar, es decir, un numero y no un vector.

Propiedades de un producto escalar:

>>Propiedad Conmutativa.

Esta propiedad indica que, no importa el orden de los factores, el resultado es el mismo.

>>Propiedad distributiva del producto escalar respecto de la suma.

Esta propiedad indica que, la suma de dos sumandos, multiplicada por un número, es igual a la suma del producto de cada sumando por ese número.

>>Propiedad Escalar.

Cuando “m” es un numero escalar, es decir, un “numero”.

Ahora ya sabiendo lo que es un producto punto y sus propiedades, te mostrare un ejemplo de como se hace un producto punto de vectores:

EJEMPLO:

Hallar si:

El producto punto no es difícil de llevar a acabo, Ya sean dos o tres vectores, solo multiplica primero los valores en “x”, después los valores en “y”, por ultimo los valores en “z”. Y al final solo nos queda sumar.