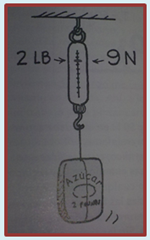
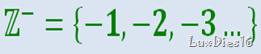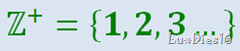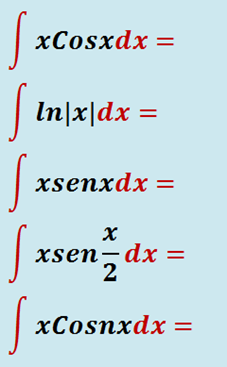Hace más de 2000 años, los antiguos científicos griegos estaban familiarizados con algunas de las ideas de la física que estudiamos en la actualidad.
-->El movimiento según Aristóteles (384-322 a. c.)
Aristóteles dividió el movimiento en dos clases principales: El movimiento natural y el movimiento violento.

Las afirmaciones de Aristóteles acerca del movimiento fueron el comienzo del pensamiento científico, y aunque él no creía que fueran definitivas acerca del tema, durante casi 2000 años sus seguidores consideraron sus ideas como fuera de toda duda. Aristóteles también decía que la Tierra no se movía, pues la Tierra debe estar en su lugar propio y como es inconcebible que haya una fuerza capaz de moverla, resultaba bastante claro que la Tierra no se movía.
-->Copérnico y la Tierra en movimiento.
En este ambiente intelectual Nicolás Copérnico (1473-1543), astrónomo polaco, formuló su teoría sobre el movimiento de la Tierra. Dedujo que la forma más sencilla de explicar los movimientos observados del Sol, la Luna y los planetas por el cielo es suponiendo que la Tierra y otros planetas describen círculos al rededor del Sol. Durante años desarrollo sus ideas sin hacerlas públicas, por dos razones fundamentales. La primera fue que tenía miedo de ser perseguido; una teoría tan distinta de la opinión común con seguridad se tomaría como un ataque al orden establecido. La segunda razón fue que él mismo tenía serias dudas, porque no podía reconciliar la idea de una Tierra en movimiento con las ideas que prevalecían acerca del movimiento. Finalmente, el los últimos días de su vida. Mandó a la imprenta su De Revolutionibus. El primer ejemplar de su famosa exposición llegó a él el día de su muerte: el 24 de mayo de 1543.
-->Galileo y la Torre inclinada.
Fue Galileo (1564-1642), el principal científico de principios del siglo XVII, quien dio crédito a la idea de Copérnico de una Tierra en movimiento. Lo logró desacreditando las ideas aristotélicas sobre el movimiento. Galileo demolió con facilidad la hipótesis de Aristóteles acerca de la caída de los cuerpos. Se dice que Galileo dejó caer objetos de varios pesos desde lo más alto de la Torre inclinada de Pisa, y luego comparó las caídas. Al contrario de la aseveración de Aristóteles, Galileo encontró que una piedra con el doble de peso que otra no caía con el doble de rapidez. A excepción del pequeño efecto de la resistencia del aire, encontró que los objetos de distinto peso, cuando se sueltan al mismo tiempo, caían untos y llegaban al suelo en el mismo momento.
--> Los planos inclinados de Galileo
Era básico para Aristóteles que un objeto requiere de un empuje o un tirón para mantenerse en movimiento. Y fue este principio básico el que rechazó Galileo al decir que si no hay interferencia para un objeto en movimiento, se mantendrá moviéndose en línea recta por siempre; no hace falta un empujón, ni tracción ni fuerza. Galileo demostró esta hipótesis experimentando con el movimiento de varios objetos sobre planos inclinados. Dedujo entonces que las esferas que ruedan por un plano horizontal ni se aceleran ni se desaceleran. La esfera llega al reposo finalmente no por su “Naturaleza”, sino por a fricción. Cuando avía menos fricción, el movimiento de los objetos duraba más. Dedujo que en ausencia de la fricción o de otras fuerzas contrarias, un objeto en movimiento horizontal continuaría moviéndose indefinidamente.
Galileo observó que una esfera, soltada desde el reposo en la parte superior de un plano inclinado hacia abajo, rodaba hacia abajo y después hacia arriba por la pendiente inclinada hacia arriba, hasta que casi llegaba a su altura inicial. Dedujo que sólo la fricción evitaba que subiera hasta llegar exactamente a la misma altura, porque cuanto más lisos fueran los planos, la esfera llegaría más cerca a la misma altura original.
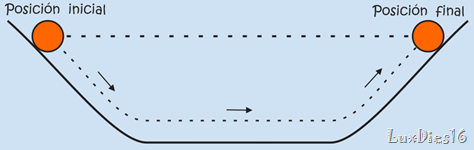
A continuación redujo el ángulo del plano inclinado hacia arriba. De nuevo la bola subió casi hasta la misma altura, pero tuvo que ir más lejos. Con reducciones adicionales del ángulo obtuvo resultados parecidos: Para alcanzar la misma altura, la esfera tenía que llegar más lejos cada vez.
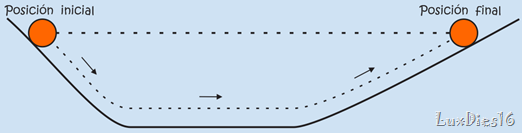
Entonces se preguntó: “si tengo un plano horizontal largo: ¿hasta donde debe llegar la esfera para alcanzar la misma altura inicial?”
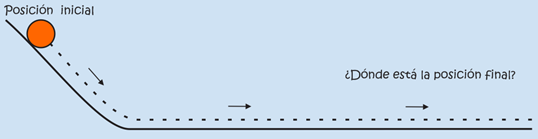
Como el movimiento de bajada de la esfera en el primer plano es igual en todos los casos, su rapidez al comenzar a subir por el segundo plano es igual en todos los casos. Si sube por una pendiente más inclinada pierde su rapidez rápidamente. En una pendiente menos inclinada la pierde con más lentitud, y rueda durante mayor tiempo. Cuanto menor sea la pendiente de subida, con más lentitud pierde su rapidez.
En el tercer caso, cuando el plano es horizontal, la esfera no debería perder rapidez alguna. En ausencia de fuerzas de retardo, la tendencia de la esfera es a moverse por siempre sin desacelerarse. A la propiedad de un objeto de resistirse a los cambios en el movimiento la llamó INERCIA.
En 1642, varios meses después de la muerte de Galileo, nació Isaac Newton. A los 23 años ya había desarrollado sus famosas leyes de movimiento, que terminaron de demoler las ideas aristotélicas que habían dominado el razonamiento de los mejores pensadores durante casi dos milenios. Estas tres leyes las puedes encontrar más detalladas en las entradas que siguen de ésta, así como también en la entrada “La Dinámica y Leyes De Newton” de física I.
Te dejo un pequeño crucigrama para que retroalimentes la información anterior.


Referencias:
Libro: Física Conceptual
Autor: Paul G. Hewitt
Editorial: Pearson Educación
Décima Edición