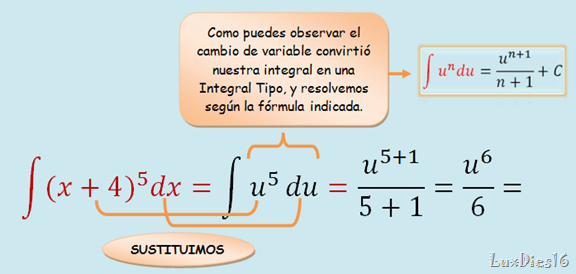
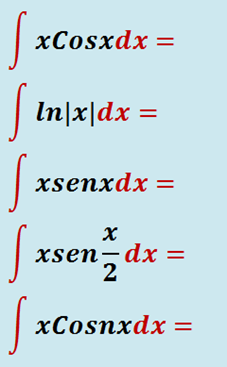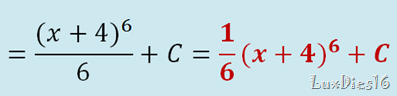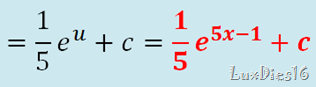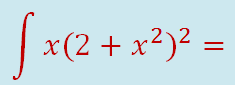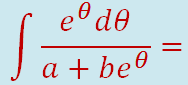La integración por partes es parecido a cambio de variable, pero un poco mas complejo así que pon mucha atención en la explicación, si te quedan dudas después de leer y releer, no dudes en contactarme, o buscar ayuda de otra fuente.
La formula anterior es muy importante para este tema, si puedes apréndetela, pero tenla siempre a la mano para realizar los ejercicios. Y solo para que no te confundas, en la primera parte de la formula
Ejemplo:
Como te avía dicho, esto es parecido al cambio de variable, Pero ahora te diré los detalles.
1.- Debes de dar un valor a u en este caso tomamos la parte del logaritmo natural (ln|x|).
2.- Ahora debes de derivar u (ln|x|) para obtener el valor de du, recuerda que la derivada de un logaritmo natural es igual a dx/n, en este caso la derivada de ln|x| es dx/x.
3.- Ahora debemos darle un valor a dv, que viene siendo el resto de la integral, es decir, ya aviamos tomado ln|x| para el valor de u, y lo que nos quedo fue xdx, así que el valor que le daremos a dv será xdx. Como consejo, elije como valor de dv, la parte de la integral que sea mas fácil de integrar.
4.- Lo siguiente es darle el valor a v, que viene siendo la integral de dv (xdx).
5.- Una vez que tenemos definidos los valores, debemos usar nuestra formula. Debes sustituir los valores tal y como te lo indica.
6.- En la formula indica que v y u se están multiplicando, tu solo indícalos, así como se muestra en la imagen.
7.- Después, se esta restando la integral del producto de v y du, igual no es necesario que los multipliques solo indícalos.
8.- Solo esta ultima integral, a continuación lo haré paso a paso.
Esta es la integral resuelta.
Bueno en esta imagen esta toda la integral resuelta, no salte ni un paso, analízala y encuentra de donde sale cada dato, por tu propia cuenta, así aprenderás mas rápido. Cuando tu maestro haga algo y no sepas porque, igual pregunta, el tendrá la respuesta.
Ejercicios:
°°~~SUERTE~~°°
