En calculo diferencial aprendimos a derivar una función y sacar su diferencial, si no lo recuerdas ahí te va un recordatorio.
Tenemos varios tipos de Funciones básicas para derivar:
Observa y Analiza esta función:
¿Recuerdas como se deriva este tipo de funciones? es de POTENCIA, siguiendo la REGLA DE CORRESPONDENCIA se deriva de esta forma:
A continuación viene un Ejemplo:
Una vez que tú tienes la derivada de una función puedes sacar su DIFERENCIAL.
Pero antes que nada debe quedarte claro que:
Entonces ahora que ya tenemos la derivada de la función, que es:
Obtendremos su diferencial, y es tan sencillo como pasar el dx multiplicando a toda la derivada, Observa.
Lo que hicimos aquí fue, el dx que dividía a d, la pasamos al otro lado multiplicando a la derivada, y LISTO, ya obtuvimos la diferencial de la función.
Básicamente, lo que tienes que hacer para obtener la diferencial de una función es primero sacar la derivada y segundo, multiplicarla con dx, y ya.
Si con esto no recuerdas nada de como derivar y diferenciar ve a las entradas de Calculo Diferencial.
Observa la siguiente imagen:
Esto quiere decir que si tú integras una diferencial, obtendrás la función original que fue derivada.
Analizando lo anterior, se puede decir que para poder integrar se debe hacer lo contrario que al derivar.
¿Como se integra?
Una vez que tu tienes una diferencial, puedes comenzar a integrarla, anteriormente vimos como derivar funciones de potencia… pues se hace lo contrario… es decir, si multiplicaste, ahora divide, si restaste ahora suma. Observa.
Esta es una integral tipo o de potencia. Es lo contrario a la derivación de una función de potencia.
Solo sigue la regla, agrégale una C y así integraras esa diferencial, y obtendrás la función original.
EJEMPLO 1:
Como puedes observar el 8 sale del símbolo de integración, esto es porque los valores constantes (números) permanecen fuera del símbolo de integración.
Si no entendiste lo analizaremos paso a paso.
Si quieres saber por qué siempre se pone la “C” al final da clic aquí.
Con esta regla de integración que hemos visto podrás hacer muchas integrales de este tipo. Te mostrare algunos ejemplos:
Ejemplo 2:
En este caso integramos termino por termino, con la regla de integración de potencia.
Como ya lo hemos visto las constantes (números) y los signos, salen del símbolo de integración y una vez que los separas comienzas a integrar normal.
Realizas la regla de integración en cada uno de ellos y al final solo divides y ya sea que lo expreses de la forma anterior o bien de la forma siguiente, da igual.
Ejemplo 3:
En este caso tenemos fracciones
, pero no te asustes es muy sencillo, solo tienes que subir lo de abajo pa’riba y colocar su exponente en negativo, para convertirlo a tipo potencia.
Ya hemos separado los términos con las constantes (números) fuera, y puedes observar que la X que se encontraba abajo ahora esta arriba con su exponente negativo.
Aquí comienzas a realizar la regla de integración, pon mucha atención en los signos, signos diferentes se restan.
Una vez que obtienes este resultado, divides, y veras que todas las fracciones quedan igual pero con signos negativos, no podemos dejar exponentes negativos así que tenemos que bajarlos pa’abajo.
Puedes observar como bajé las X negativas y sus exponentes cambian a positivos, y los 1 con coeficientes (letra) no son necesarios escribirlos.
Esto solo fue una introducción así que si quieres seguir integrando ve a la siguiente entrada de Cálculo Integral.
EJERCICIOS:
Se integra factor por factor.
La raíz sube como exponente de 1/2
Desarrolla el binomio al cuadrado.
Lo de abajo sube pa’riba.
Igual que la anterior lo de abajo sube pa’riba.





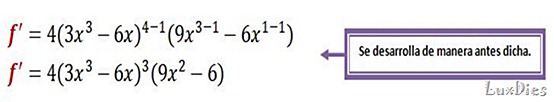


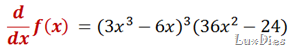

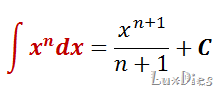
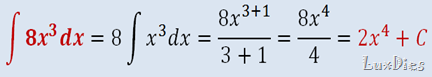

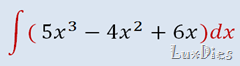



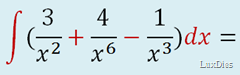



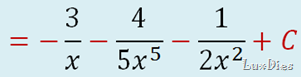
![ni%F1o%20estudiando[3] ni%F1o%20estudiando[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiSh82Gc4bWSU66PAr8-l9JJ6CNJnOoMLAK33p_RTfjZSa2fRvxlV7_4UQDyU2bPiFzWUm4yhWdHHGobKo6oi8yGsjfw8cJNd7MZZUK2Br5hjKSmfnxuF3QX-inmsf7-m6askXqgmE3tvQ/?imgmax=800)
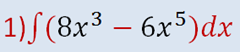




No hay comentarios:
Publicar un comentario