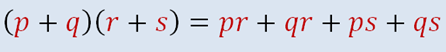Mundo Estudiante: Cálculo

Mostrando entradas con la etiqueta Cálculo. Mostrar todas las entradas

Propiedades De Los Números Reales

A continuación veremos las propiedades de los números reales, yo te recomiendo que leas con atención y trates de entenderlo lo mejor posible, pues y te aseguro que tan solo con saber estas propiedades, te será más sencillo resolver ciertas operaciones un un futuro.

-->Propiedad Conmutativa:

En la adición (suma) y en la multiplicación el orden es intrascendente es decir:

No importa que posición tengan, el resultado es el mismo.

-->Propiedad Asociativa:

La agrupación en la suma o multiplicación de mas dé dos números reales, no afectará el resultado final, es decir:

No importa como lo agrupes, el resultado será el mismo.

-->Propiedad Distributiva:

La multiplicación de un número y una suma de dos números es equivalente a multiplicar cada uno de los dos números por el número y luego sumar los productos. Es decir:

Como la misma palabra lo indica, puedes “distribuir” el número de afuera en los de adentro, sin ignorar el signo que los suma.

-->Elemento Neutro o Identidad:

Es el elemento que al operarlo bajo la suma o la multiplicación con cualquier número real, produce o da como resultado el mismo número real respectivamente.

Simple y sencillamente es, el número que multiplicado o sumado, con x número, te da como resultado el x número.

-->Inverso:

Es el elemento que al operarlo con un número real bajo la suma o multiplicación da como resultado el elemento identidad de cada operación respectivamente.

Bueno ahora vamos a la mitad de las propiedades, te voy a dar un ejemplo de como identificar una propiedad en una operación, y de esta forma se te facilitará realizar operaciones llevando a cabo las propiedades pasadas.

--> Si p, q, r, y s denotan números reales demuestre :

Muy bien ahora debemos de demostrar qué propiedad se utilizó para llegar a este resultado.

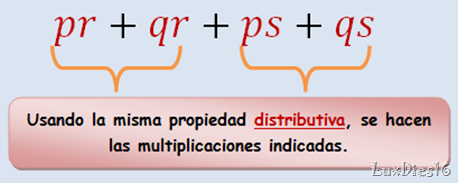
Y hemos terminado, se realizaron dos procedimientos de la propiedad distributiva para poder llegar al resultado. Si aun no entendiste, te recomiendo que analices las imágenes, ve sus diferencias.

Ahora te voy a poner algunos ejercicios, parecidos al anterior, lo único que debes hacer es identificar la propiedad que se usó.

Ejercicios:

a) 7+10=10+7

b) 2x(3+y)=(3+y)2x

c) 2(a+b)=2a+2b

d) (x+2y)+2z=x+(2y+3z)

Ahora realiza la propiedad indicada:

Distributiva –> 5x+5y

Asociativa –> 7(3x)

Las propiedades que faltan las encuentras en la siguiente entrada.

~~SUERTE~~

Algebra y Número Reales

¿ALGEBRA?

Es la rama de las matemáticas que estudia los números y las operaciones que con ello se realizan de la forma más general posible, utilizando letras y números.

Conjunto de los números Reales

Los números reales se emplean en toda la matemáticas por lo que resulta útil clasificar los diferentes tipos de números que manejamos.

--> NATURALES

Son aquellos números que nacieron de la necesidad de contar o enumerar, este conjunto se denota por: En otras palabras son los números del 1 al infinito.

--> ENTEROS

Son una generalización del conjunto de los números naturales, incluye al cero y los enteros negativos, dicho conjunto se denota por , el cual esta formado por:

--> RACIONALES

Se llaman números racionales a todo número que puede expresarse como el cociente de dos enteros con denominador distinto de cero. Es decir:

En ocasiones los números racionales se expresan como decimales finitos (son aquellos que tienen fin, es decir, no hay un número que se repita.) o decimales infinitos periódicos (son aquellos números que no se acaban, es decir, hay uno o varios números que se repiten infinitamente. Por ejemplo: 0,333333.....). El conjunto de los números racionales se denotan por

--> IRRACIONALES

Son aquellos que no pueden expresarse de manea fraccionaria, o tienen cifras decimales infinitas no periódicas tales como:

--> REALES

Pueden expresarse en forma de decimal mediante un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas en otras palabras todas las clasificaciones anteriores forman parte del conjunto de los números reales los cuales se denotan por

_____________________________________________

--> IMAGINARIOS

Un número imaginario es un número cuyo cuadrado es negativo. Cada número imaginario puede ser escrito como bi donde b es un número real e i es la unidad imaginaria.

--COMPLEJOS

Es un numero complejo de dos partes, un número real y un número imaginario, conectados por la suma de la forma a+bi, dicho conjunto se denota por .

Esquema del conjunto de los números reales:

EJERCICIOS:

CLASIFICA LOS SIGUIENTES NÚMEROS SEGUN LOS CONCEPTOS Y ESQUEMA ANTERIORES:

EJEMPLO:

-6 --> ,,

-->

Integración Por Partes

La integración por partes es parecido a cambio de variable, pero un poco mas complejo así que pon mucha atención en la explicación, si te quedan dudas después de leer y releer, no dudes en contactarme, o buscar ayuda de otra fuente.

La formula anterior es muy importante para este tema, si puedes apréndetela, pero tenla siempre a la mano para realizar los ejercicios. Y solo para que no te confundas, en la primera parte de la formula se refiere a la integral que vas a hacer, el resto es lo que tienes que hacer para poder realizarla. Ahora te explicare un ejemplo.

Ejemplo:

Como te avía dicho, esto es parecido al cambio de variable, Pero ahora te diré los detalles.

1.- Debes de dar un valor a u en este caso tomamos la parte del logaritmo natural (ln|x|).

2.- Ahora debes de derivar u (ln|x|) para obtener el valor de du, recuerda que la derivada de un logaritmo natural es igual a dx/n, en este caso la derivada de ln|x| es dx/x.

3.- Ahora debemos darle un valor a dv, que viene siendo el resto de la integral, es decir, ya aviamos tomado ln|x| para el valor de u, y lo que nos quedo fue xdx, así que el valor que le daremos a dv será xdx. Como consejo, elije como valor de dv, la parte de la integral que sea mas fácil de integrar.

4.- Lo siguiente es darle el valor a v, que viene siendo la integral de dv (xdx).

5.- Una vez que tenemos definidos los valores, debemos usar nuestra formula. Debes sustituir los valores tal y como te lo indica.

6.- En la formula indica que v y u se están multiplicando, tu solo indícalos, así como se muestra en la imagen.

7.- Después, se esta restando la integral del producto de v y du, igual no es necesario que los multipliques solo indícalos.

8.- Solo esta ultima integral, a continuación lo haré paso a paso.

Esta es la integral resuelta.

Bueno en esta imagen esta toda la integral resuelta, no salte ni un paso, analízala y encuentra de donde sale cada dato, por tu propia cuenta, así aprenderás mas rápido. Cuando tu maestro haga algo y no sepas porque, igual pregunta, el tendrá la respuesta.

Ejercicios:

°°~~SUERTE~~°°

Cambio De Variable

Se llama Integral Tipo a una formula de integración donde U representa una función de X

¿A que se refiere con esto? Antes de mostrarte una ejemplo, en la siguiente imagen puedes observar las tres casos de Integral Tipo, puedes notar que en el primer caso es básicamente igual a la forma de integración que se muestra en el tema de INTRODUCCION A CALCULO INTEGRAL, así que no será tan complicado comprender.

Integral Tipo Caso 1:

Lo siguiente es sustituir los valores por u y du…

Por ultimo sustituimos el verdadero valor de u…

Puede quedar de las dos formas, ya que viene siendo lo mismo, la diferencia es que en la primera el 1/6 ya esta multiplicado, y en el otro solo esta señalado que se esta multiplicando. Y hemos terminado.

Integral Tipo Caso 2: