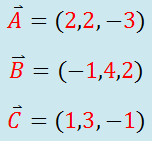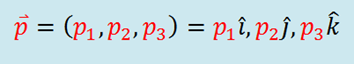Recordemos que la palabra producto en términos matemáticos se refiere al resultado de multiplicar dos factores, pero en el caso de los vectores obtener su producto no es igual que al multiplicar dos números cualesquiera.
Se subdivide en varios productos:
a) Producto Escalar o interno (punto). Dados dos vectores A y B, su producto escalar o interno, A.B, se define como el producto de sus módulos por el coseno del ángulo que forman.
Por lo tanto:
Recuerda que el producto punto siempre será un escalar, es decir, un numero y no un vector.
Propiedades de un producto escalar:
>>Propiedad Conmutativa.
Esta propiedad indica que, no importa el orden de los factores, el resultado es el mismo.
>>Propiedad distributiva del producto escalar respecto de la suma.
Esta propiedad indica que, la suma de dos sumandos, multiplicada por un número, es igual a la suma del producto de cada sumando por ese número.
>>Propiedad Escalar.
Cuando “m” es un numero escalar, es decir, un “numero”.
Ahora ya sabiendo lo que es un producto punto y sus propiedades, te mostrare un ejemplo de como se hace un producto punto de vectores:
EJEMPLO:
El producto punto no es difícil de llevar a acabo, Ya sean dos o tres vectores, solo multiplica primero los valores en “x”, después los valores en “y”, por ultimo los valores en “z”. Y al final solo nos queda sumar.
EJERCICIOS:
Realiza las siguientes operaciones si:
***SUERTE***